 V )
V )
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
Ce premier exemple vous a permis d’appréhender la notion de système de Lindenmayer sans toutefois peut-être
discerner comment nous allons utiliser cela concrètement avec la tortue.
C’est là que cela devient intéressant : Chacun des mots ainsi construits ne possède pas de signification particulière.
On va alors attacher à chacune des lettres de la séquence, une commande à exécuter par la tortue et générer ainsi
des dessins en 2D ou en 3D.
 V )
V )
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
Prenons par exemple α = 90 et un déplacement unitaire de 10 pas de tortue, on obtient alors :
| Symbole | F | + | - | & | ^ | \ | ∕ | | |
| Commande XLogo | av 10 | tg 90 | td 90 | pique 90 | cabre 90 | rg 90 | rd 90 | td 180 |
Considérons le L-system :
Premières itérations :


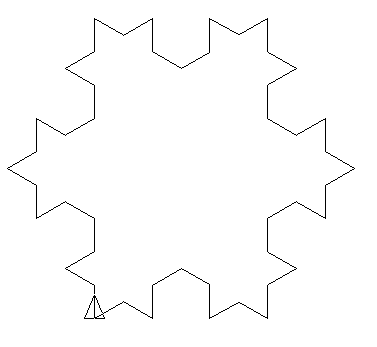
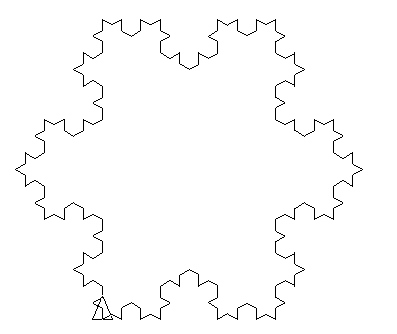
Programme en Logo :
Intéressons-nous le L-system suivant :
Voici les premières représentations en utilisant α = 90 et en ajustant le pas unitaire de telle sorte que la figure fasse toujours la même taille :




Il est alors très facile de créer le programme Logo permettant de générer ces dessins :
A → A + B+ |
B →-A - B |

dragon 10

dragon 15
L’exemple suivant traite de la courbe de Hilbert dans l’espace, c’est une courbe qui a la propriété de remplir
parfaitement un cube quand on augmente le nombre d’itérations.
Voici le L-system associé :
A → B - F + CFC + F - D&F^D - F + &&CFC + F + B∕∕ |
B → A&F^CFB^F^D^^ - F - D^|F^B|FC^F^A∕∕ |
C →|D^|F^B - F + C^F^A&&FA&F^C + F + B^F^D∕∕ |
D →|CFB - F + B|FA&F^A&&FB - F + B|FC∕∕ |
Et les premières itérations obtenues :



